$$\def\dd{\text d}$$
今年的五一劳动节过的名副其实. 节前,与几个小同学讨论他们做的一个题目,在没有准备的情况下,讲了一下一个盒子中放了若干个硬球的速度(或动量)分布的推导。
系统的能量是给定的,这样就有一个约束关系,即所有硬球的动能加起来守恒,写出来就是
$$
\sum_{i=1}^N \vec p_i^2 = 2mE \qquad (1)
$$
按照等概率假定,在此约束条件下,每个可能的微观状态有相同的概率。现在要求单粒子动量分布,这只要把常数的概率对于除一个硬球的动量外的其他动量积分即可,也就是对$N-1$个硬球的动量在(1)式的限制下积分。若对$\vec p_2, \vec p_3, \cdots, \vec p_N$积分,限制条件成为
$$
\sum_{i=2}^N \vec p_i^2 = 2mE -\vec p_1^2 \qquad (2)
$$
若系统所在的空间维数是$D$, (2)式是一个$D(N-1)$维空间的球面,球的半径$R =\sqrt{2mE -\vec p_1^2}$, 所以,积分的结果就是这个球的面积,正比于 $R^{D(N-1)-1}$,于是,单粒子动量分布就是
$$
f(\vec p) = C (2mE-\vec p^2)^{d(N-1)/2-1/2} \qquad (3)
$$
$C$由归一化条件决定,即要求
$$
\int f(\vec p) \text{d}^D \vec p =1
$$
这基本上就是我当时所讲的内容。然后,看一下$D=2$, $N=2$的情形,此时(3)成为
$$
f(\vec p) = C (2mE-\vec p^2)^{1/2}
$$
这个结果是错的(第一次错误)!!为什么会错?当时没有想清楚。只好告诉同学,等想清楚了再告诉他们为什么是错的。
实际上,这个错误本来是不会犯的,给定能量,等概率的分布与$\delta(E-H)$成比例,当时问了一下几位小朋友,他们还没有学到$\delta$函数,于是就想回避$\delta$函数,结果算错了。当然,可以回避$\delta$函数,这就是刘全慧老师推荐过的,发表在大学物理上的李洪芳老师等的文章中的做法,把确定能量的约束条件看成是能量处于一个$\Delta E$的范围,再令$\Delta E \to 0$,这大致是所谓微正则系综的标准做法。为什么直接在球面上积分就错了呢?给定了能量,把系统的动量限制在一个$DN$维空间的球面上了,$N$个粒子的动量,有$DN$个,所以对应的体积元是$DN$维。微观状态是定义在$DN$维空间上,即$DN$维空间的一个“点”为一微观状态。为了确切定义,这个点应该是有大小的,而有大小的点无法嵌入到低一维的面上去。如果非要在低一维的面上做事情,就得用$\delta$函数,这个函数自狄拉克引进后,如今已经很平常了。直接在球面上积分,相当于是固定了球的半径,而固定能量,给定的是球的半径的平方。直观的看,这是等价的,但是,计算的结果并不一样,后面的具体计算中会看到这个差别。这样,$N$个粒子的分布函数应写成
$$
P(\vec p_1, \vec p_2, \cdots, \vec p_N) \propto \delta(\sum_{i=1}^N \frac{\vec p_i^2}{2m} -E)
$$
对$\vec p_2, \vec p_3, \cdots, \vec p_N$积分即得单粒子动量分布。令 $$X = \sqrt{\vec p_2^2 +\vec p_3^2 + \cdots +\vec p_N^2}$$则
$$
\begin{aligned}
\delta(\sum_{i=1}^N \frac{\vec p_i^2}{2m} -E)= &2m \delta(X^2 +\vec p_1^2 – 2mE) \\
= &\frac{m}{\sqrt{2mE-\vec p_1^2}}(\delta(X-\sqrt{2mE-\vec p_1^2})+\delta(X+\sqrt{2mE-\vec p_1^2})) \\
\dd^D\vec p_2 \cdots \dd^D\vec p_N = &X^{D(N-1)-1}\dd X\dd\Omega_{D(N-1)}
\end{aligned}
$$
$\dd \Omega_{D(N-1)}$是$D(N-1)$维空间的球面角元。如果是对球面积分,相当于是用了$\delta(X-\sqrt{2mE-\vec p_1^2})$,少了一个$\sqrt{2mE-\vec p_1^2}$的分母。
完成积分, 得到单粒子动量分布
$$
f(\vec p) = C_D (2mE-\vec p^2)^{D(N-1)/2-1}
$$
$C_D$由归一化条件决定。 $D=2$时,
$$
f(\vec p) = C_2 (2mE-\vec p^2)^{N-2}
$$
$D=3$时
$$
f(\vec p) = C_3 (2mE-\vec p^2)^{(3N-5)/2}
$$
分布仅与$\vec p$的大小有关,对角度积分,得到动量大小的分布。$D=2$时,
$$
f(p) =2\pi C_2 p (2mE- p^2)^{N-2}
$$
$D=3$时
$$
f(p) = 4\pi C_3 p^2 (2mE- p^2)^{(3N-5)/2}
$$
由归一化关系
$$
\frac1{2\pi C_2} = \int_0^{\sqrt{2E/m}} p (2mE- p^2)^{N-2} \dd p =\frac1{2(N-1)}(2mE)^{N-1}
$$
$$
\frac1{4\pi C_3} = \int_0^{\sqrt{2E/m}} p^2 (2mE- p^2)^{(3N-5)/2} \dd p
$$
令 $ x = \frac{mp^2}{2E} $,
$$
\begin{aligned}
\frac1{4\pi C_3} = & \frac12(2mE)^{3N/2-1} \int_0^1 x^{3/2-1}(1-x)^{3(N-1)/2-1} \dd x \\
=&\frac12(2mE)^{3N/2-1} B(\frac32, \frac{3(N-1)}{2}) \\
= & \frac12(2mE)^{3N/2-1} \frac{\Gamma(\frac32)\Gamma(\frac{3(N-1)}{2})}{\Gamma(\frac{3N}{2})} \\
=&\frac{\sqrt{\pi}}4 (2mE)^{3N/2-1} \frac{ \Gamma(\frac{3(N-1)}{2})}{\Gamma(\frac{3N}{2})}
\end{aligned}
$$
最后得到, $D=2$时
$$
f(\vec p) = \frac{(N-1)} {\pi(2mE)^{N-1}} (2mE-\vec p^2)^{N-2}
$$
$$
f( p) = \frac{2(N-1)}{(2mE)^{N-1}} p(2mE- p^2)^{N-2}
$$
$D=3$时
$$
f(\vec p) = \frac{1}{ \pi^{3/2} (2mE)^{3N/2-1}} \frac{\Gamma(\frac{3N}{2})}{ \Gamma(\frac{3(N-1)}{2})} (2mE-\vec p^2)^{(3N-5)/2}
$$
$$
f(p) = \frac{4}{\pi^{1/2} (2mE)^{3N/2-1}} \frac{\Gamma(\frac{3N}{2})}{ \Gamma(\frac{3(N-1)}{2})} p^2 (2mE- p^2)^{(3N-5)/2}
$$
特别的, 当$D=2$, $N=2$时
$$
f(\vec p) = \frac1{2\pi m E}, \quad f(p) = \frac{1}{mE} p
$$
这是正确的解果。由上述结果,很容易得到能量分布, $D=2$时
$$
f(\varepsilon) = \frac{(N-1)}{E^{N-1}} (E- \varepsilon)^{N-2}
$$
$D=3$时,
$$
f(\varepsilon) = \frac{2}{\sqrt{\pi} E^{3N/2-1}} \frac{\Gamma(\frac{3N}{2})}{ \Gamma(\frac{3(N-1)}{2})} \sqrt{\varepsilon} (E- \varepsilon)^{(3N-5)/2}
$$
$D=2$, $N=2$时
$$
f(\varepsilon) = \frac{1}{E }
$$
$D=2$, $N=3$时
$$
f(p)=\frac{1}{(mE)^2} p(2mE -p^2), \quad f(\varepsilon) = \frac{2}{E^2} (E-\varepsilon)
$$
在得到这些结果之后,恰好是劳动节。反正闲着也是闲着, 就花了一天时间,写了一段c代码,打算用分子动力学模拟检验一下这个结果。在李洪芳老师等的文章中,先有分子动力学模拟结果,然后是推导。但是,也许那个年代的计算机算力有限,李老师的结果中能看到明显的统计误差。现在的任何一台计算机,都能很快算出统计误差很小的结果,这只需要算得时间长一点即可。经过几次调试,就开始出结果了。先丢掉了$10^6$碰撞,然后每$20$次碰撞取一次数据,并统计数据得到若干个所求的分布。在整个变量区间,取了100个子区间,是李洪芳老师的25个子区间的4倍。能量分布的结果如下图,图中同时画出了理论结果。计算中取$m=1$,总能量$E=N$,这里$N=2$,即$E=2$。
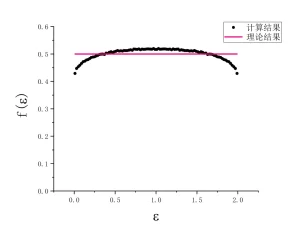
由图可见, 计算结果和理论结果之间有明显差别, 而且,这个差别显然不是统计误差,这里的计算,取样数为$10^8$的数量级,统计误差大体为$10^{-4}$的量级。应该是什么地方出错了,如果没有错误,这将是一个重要发现,因为这表明遍历性发生了破缺,而长方框子中的两个硬盘子应该已经被数学家证明是遍历的。所以,一定是我算错了(第二次错误!)。把粒子数改为$N=3, 4, 5$等等, 计算结果与理论结果的差别从图上看已不明显,但如果把计算结果和理论结果之差画出来,则仍然可以判定二者之差不是统计误差。
此后两天,仔细检查代码,没有找到错误。
根据经验,不停地找下去,非明智之举。遂放在一边,打算过几天再来检查。但这个诡异的结果,总是在脑子里挥之不去。直到前天早晨醒来,突然意识到错误出在何处。爬起来,只需要改写几行代码,二分钟搞定,编译,提交计算。刷牙,洗脸,喝了一杯牛奶,计算已经结束。立刻画图,图在下面。
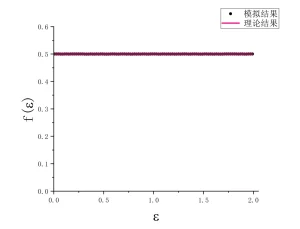
模拟结果和理论结果几乎重合,把两个结果之差画出来,是合理的统计误差。误差对于$\varepsilon$和$E-\varepsilon$对称,这是因为计算中能量给定为$E$,在每个取样中,$\varepsilon$和$E-\varepsilon$ 同时出现。
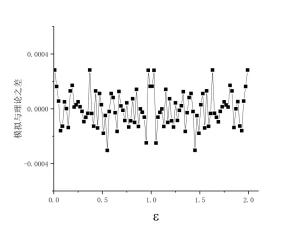
最后,揭秘错误。这是一个非常非常初等的愚蠢错误,错在取样方法。分子动力学计算中,物理量的平均值是时间平均,所以正确的做法是以等时间隔取样。而错误的原因是以等碰撞间隔取样。对于两个盘子,盘子与框子边的碰撞次数比两个盘子互碰的次数要多,而与框子边的碰撞不改变盘子速度的大小,当两个盘子速度差不多时,在相等时间间隔内与框子边的碰撞次数比两个盘子速度相差较大时要多,这就是导致错误的原因。当粒子数增加时,与框子边的碰撞次数相对于盘子之间的碰撞次数变小,所以,等碰撞次数取样与等时间间隔取样的差别变小。
这样一个小题目,两步都做错了,再经过反复才做对,实属不易。以前做题目,几乎每次都会犯点错误,但大部分步骤还是对的。而每一步都错,似乎还是第一次碰到。写出来,做个记录。30多年前,也曾经有过一次错误和教训,过一阵再爆。
一个题目做错一步并不难,难的是每一步都做错,一错到底。

有趣!